概率密度估计

今天来理一下概率密度、概率密度函数、概率密度估计和核密度估计之间的关系，并介绍如何用Python绘制直方图，求解核密度估计。

概率密度

首先，介绍一下概率密度（Probability density, PD），它用来表示观测值和其概率之间的关系。概率是面积，概率密度是单位观测值的概率，即概率密度=概率/随机变量的单位。概率密度的总体形状被称为概率分布。

概率密度函数

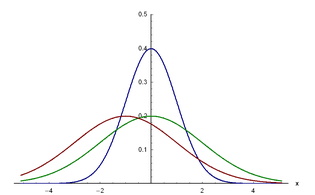
其次，什么是概率密度函数（Probability density function，PDF），它有时也称为密度函数，概率分布函数。是一个连续分布函数的导数，指一个值到它的概率密度的函数映射。直观上来看，是将直方图的组距切割得越来越细，观察其顶部逐渐接近一条曲线，这条曲线就是概率密度函数的图形。（参考概率密度函数）如图1所示，为正态分布的概率密度函数，横轴为随机变量的取值，纵轴为概率密度函数的值，随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。当概率密度函数存在时，累积分布函数（CDF）是概率密度函数（PDF）的积分。（参考概率密度函数）

正态分布的概率密度函数.png

图1：正态分布的概率密度函数

概率密度估计

接着，那什么又是概率密度估计（Probability density estimation, PDE）呢？通常是在不知道一个随机变量的PDF，需要去逼近这个PDF，这个逼近的过程就是概率密度估计。概率密度估计的步骤为：

  1. 用一个直方图来检查随机样本中观测值的密度，从直方图可以大致看出数据服从什么样的分布，如正态分布等。如果看不出明显的分布，则需要构建一个模型来估计分布；
  2. 估计分布的参数，也叫做参数密度估计；
  3. 针对数据样本不符合常见的概率分布时，则需要采用非参数密度估计（使用所有样本来进行密度估计），常见的非参数密度估计方法包括核平滑法（Kernel smoothing）或核密度估计（Kernel density estimation, KDE）。

非参数密度估计包含2个重要的参数，平滑参数（Smoothing parameter）和核函数（Kernel function）。（参考概率密度估计介绍）

核密度估计

然后，介绍下非参数密度估计中的一类重要方法，核密度估计（Kernel density estimation, KDE）。它是一种非参数估计方法，针对于数据样本不符合常见的概率分布，需要使用所有样本来进行密度估计。‘核’可以理解为一个函数，用来提供权重。在网上看到一种理解，挺有意思。那就是核密度函数是一种“平滑（smooth）”的手段，相当于说“我说我很牛逼你可能不信，但是你可以听我的朋友们怎么评价我的，加权平均下就能更好地了解我了”。

设$(x_1,x_2,…,x_n)$是独立同分布的$n$个样本点，它的概率密度函数是$f$，于是核密度估计函数为：
$$\hat{f}h(x)=\frac{1}{n} \sum{i=1}^n K_h\left(x-x_i\right)=\frac{1}{n h} \sum_{i=1}^n K\left(\frac{x-x_i}{h}\right)$$
其中$h$是人为设定的，叫作平滑参数（smoothing parameter），也叫作带宽（bandwidth）。

用Python绘制直方图，求解核密度估计

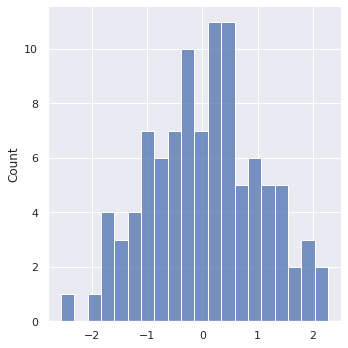
  • 用Python的数据可视化库matplotlib和seaborn绘制直方图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import seaborn as sns

import numpy as np

import matplotlib.pyplot as plt


sns.set()

np.random.seed(0)

x = np.random.randn(100)

### plot the hist in seaborn
sns.displot(x, bins=20, kde=False, label='sns.histplot')

plt.show()

直方图.png

图2：绘制的直方图
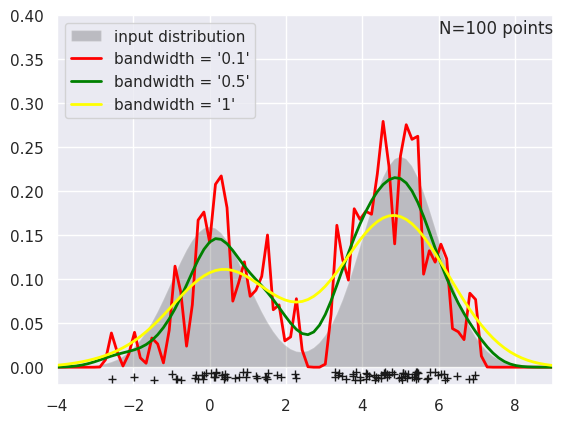
  • 用Python的Scikit-learn库计算、绘制核密度估计图。还可以使用Scipy，Statsmodels库。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from scipy.stats.distributions import norm

from sklearn.neighbors import KernelDensity


N = 100

np.random.seed(0)

X = np.concatenate((np.random.normal(0, 1, int(0.4 * N)), np.random.normal(5, 1, int(0.6 * N))))[:, np.newaxis]

X_plot = np.linspace(-5, 10, 100)[:, np.newaxis]

true_dens = (0.4 * norm(0, 1).pdf(X_plot[:, 0]) + 0.6 * norm(5, 1).pdf(X_plot[:, 0])) 

fig, ax = plt.subplots()

ax.fill(X_plot[:, 0], true_dens, fc='black', alpha=0.2, label='input distribution')

colors = ['red', 'green', 'yellow']

bws = [0.1, 0.5, 1]

lw = 2

for color, bw in zip(colors, bws):

        kde = KernelDensity(kernel='gaussian', bandwidth=bw).fit(X)

        log_dens = kde.score_samples(X_plot)

        ax.plot(X_plot[:, 0], np.exp(log_dens), color=color, lw=lw,

                linestyle='-', label="bandwidth = '{0}'".format(bw))

ax.text(6, 0.38, "N={0} points".format(N))  

ax.legend(loc='upper left')

ax.plot(X[:, 0], -0.005 - 0.01 * np.random.random(X.shape[0]), '+k')

ax.set_xlim(-4, 9)

ax.set_ylim(-0.02, 0.4)

绘制的核密度估计图.png

图3：绘制的不同bandwidth下的核密度估计图

参考资料

  1. 概率密度函数
  2. 维基百科-概率密度函数
  3. 概率密度估计介绍
  4. 绘制直方图与求解核密度估计的Python方法

欢迎各位提出建议、问题，我们一起交流、学习、成长。

“问渠那得清如许？为有源头活水来” ヾ(◍°∇°◍)ﾉﾞ

– 我在半亩方塘等你 ^_^