【论文笔记-4】Attention Is All You Need

Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. “Attention is all you need.” In Advances in neural information processing systems, pp. 5998-6008. 2017.

简介

RNN、LSTM和GRU在序列建模、语言建模和机器翻译等领域被广泛应用。大量的工作来研究如何突破循环语言模型和编码器-解码器模型之间的界限。循环模型通常沿着输入和输出序列的符号位置进行因子计算。在计算时间中将位置与步骤对齐，生成隐含状态$h_t$的一个序列，作为先前的隐含状态$h_{t-1}$和位置$t$的输入的函数。这种固有的顺序特性妨碍了训练样本的并行化，而在较长的序列长度下，并行化就变得至关重要，因为内存约束限制了样本之间的批处理。最近的工作通过因子分解技巧和条件计算在计算效率上取得了显著的提高，同时也提高了后者的模型性能。然而，顺序计算的基本约束仍然存在。

注意力机制已经成为序列建模和转换模型中引人注目的一个组成部分，允许建模依赖关系而不考虑它们在输入或输出序列中的距离。除了少数情况外，注意力机制往往与循环神经网络一起使用。

在文章中，作者提出了Transformer模型，该模型避免了循环，而完全依赖于一个注意力机制来刻画输入和输出之间的全局依赖关系。

Transformer可以实现更大程度的并行化，在8块P100 GPU上只训练了12个小时，就可以在翻译质量方面达到一个新的水平。

模型结构

大多数的经典神经序列转换模型都有一个编码器-解码器的结构。编码器将一个符号表示的输入序列$(x_1,…,x_n)$映射成连续表示的序列$z=(z_1,…,z_n)$。给定$z$，解码器接下来生成符号表示的输出序列$(y_1,…,y_m)$，每次生成一个元素。在每一步，模型都是自回归的，在生成下一个符号时，使用先前生成的符号作为附加输入。Transformer模型沿袭了这种结构，在编码器和解码器中使用堆叠的自注意力、逐点的和全连接层，如下图所示，左边是编码器，右边是解码器。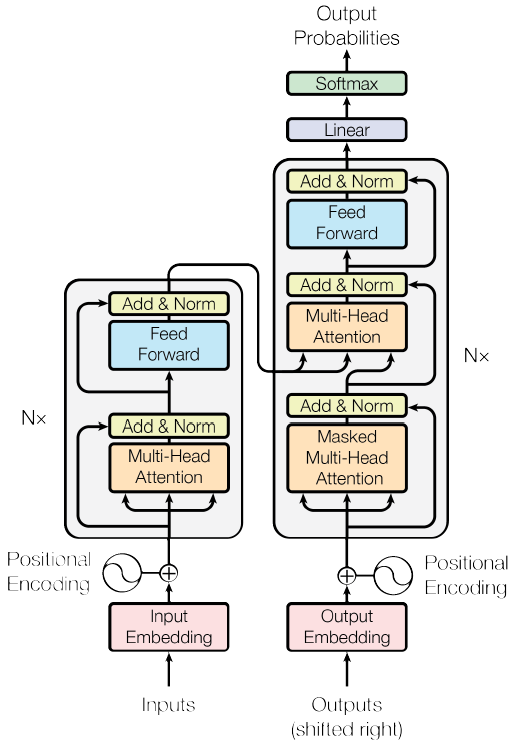

编码器和解码器

编码器部分： 编码器由6个相同的层堆叠组成。每层有两个子层，由下往上，第一层是一个多头自注意力机制，第二层是逐点式的全连接前馈网络。在每个子层上使用一个残差连接，然后进行层规范化（layer normalization）。也就是说每个子层的输出是LayerNorm($x$+Sublayer($x$))。

解码器部分： 解码器也由6个相同的层堆叠组成。除了编码器的两个子层，解码器还加入了第三个子层，这个子层在编码器的输出上执行多头注意力操作。与编码器类似，解码器也会在每个子层上使用一个残差连接，然后进行层规范化。修改了解码器堆栈中的自注意力子层，以防止位置注意到后续位置。这个修改，是基于输出嵌入有一个位置偏移的事实考虑，确保了对位置$i$的预测只能依赖于小于$i$的已知输出。

注意力机制

注意力机制函数可以被描述成将查询（query）、键（key）、值（value）映射到一个输出，其中查询、键、值和输出都是向量。输出以值的加权和的形式计算，其中分配给每个值的权重由查询与相应键的兼容函数计算。

按比例的点积注意力（Scaled Dot-Product Attention）

按比例的点积注意力结构如下图所示。输入包括$d_k$维的查询和键，以及$d_v$维的值。计算公式是$Attention(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V$。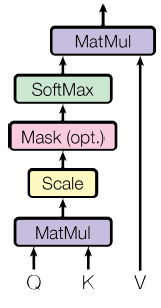

多头注意力 (Multi-Head Attention)

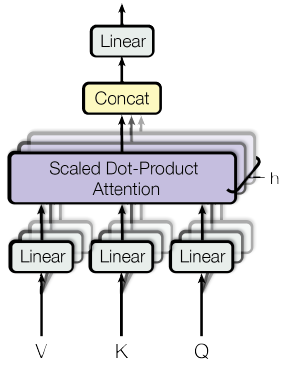
与使用$d_{model}$维的键，值，查询执行单一注意力函数不同，作者发现使用不同的学习线性投影将查询，键，值投影到$d_k, d_k, d_v$维是有益的。然后，对每一个查询、键和值的投影版本并行执行注意力函数，生成$d_v$维的输出值。它们被连接起来并再次投影，从而产生最终的值。如下图所示。多头注意力使模型能够在不同的表示子空间中，在不同的位置共同关注信息。计算公式是
$$
\begin{aligned}
\text { MultiHead }(Q, K, V) &=\text { Concat }\left(\text { head }{1}, \ldots, \text { head }{\mathrm{h}}\right) W^{O} \
\text { where head }{\mathrm{i}} &=\text { Attention }\left(Q W{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right)
\end{aligned}
$$

其中，投影是参数矩阵，$W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}$，$W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}$，$W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}}$ and $W^{O} \in \mathbb{R}^{h d_{v} \times d_{model}}$。本文中采用了$h=8$个分布式的注意力层（头），每层的$d_k=d_v=d_{model}/h=64$。由于每个头的维数降低，其总计算代价与全维单头关注的计算代价相似。

注意力机制在模型中的应用

在“编码器-解码器注意力”层中，查询来自前一解码器层，键和值来自编码器的输出。
编码器包含子注意力层。在自注意力层中，所有的键、值和查询都来自相同的位置，在本例中是编码器中前一层的输出。所述编码器中的每个位置都可以顾及所述编码器的前一层中的所有位置。
解码器中的自注意力层允许解码器中的每个位置关注解码器中的所有位置，直到并包括该位置。

逐点式的前馈神经网络

这部分包括两个线性转换，中间有一个ReLU激活函数。计算公式是
$$
\mathrm{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2}
$$

Embedding and Softmax

与其他序列转换模型类似，使用学习到的嵌入将输入符号和输出符号转换为$d_{model}$维的向量。也使用通常学习到的线性变换和Softmax函数将解码器的输出转换为预测的下一个符号的概率。

位置编码

由于本模型不包含循环和卷积，为了让模型利用序列的顺序，必须注入一些关于序列中符号的相对或绝对位置的信息。因此，在编码器和解码器堆栈底部的输入嵌入中添加了“位置编码”。位置编码与嵌入具有相同的$d_{model}$维数，因此可以将两者相加。在本文中，使用了不同频率的正弦和余弦函数，如公式所示
$$
\begin{aligned}
P E_{(p o s, 2 i)} &=\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \
P E_{(p o s, 2 i+1)} &=\cos \left(\text { pos } / 10000^{2 i / d_{\text {model }}}\right)
\end{aligned}
$$
其中，$pos$是位置，$i$是维数。也就是说，位置编码的每一维对应一个正弦信号。

小结

在这项工作中，提出了Transformer，这是第一个完全基于注意力机制的序列转换模型，用多头自注意力取代了编码器-解码器结构中最常用的循环层。对于翻译任务，Transformer的训练速度比基于循环层或卷积层的架构要快得多。